Rotated Table Illusion

Roger Shepard's Rotated Table Illusion
Visually elaborated
(DRAFT: Liable to change)

Aaron Sloman
http://www.cs.bham.ac.uk/~axs
School of Computer Science, University of Birmingham.

Installed: 3 Feb 2013
Last updated: 3 Feb 2013, 19 Sep 2016; 20 Nov 2016
This document is
http://www.cs.bham.ac.uk/research/projects/cogaff/misc/rotated-table-illusion.html

A partial index of discussion notes is in
http://www.cs.bham.ac.uk/research/projects/cogaff/misc/AREADME.html

Previous versions of the illusion online

Shepard's original table illusion was something like this (without the coloured rectangles):
-- Available at https://www.ncbi.nlm.nih.gov/pmc/articles/PMC3485780/figure/F1/
-- Copyright: © 2011 C W Tyler
The two table tops look as if they have different shapes. But the shapes in the image are identical. The coloured rectangles are provided to help convince the viewer, but you may have to hold a measuring device against the screen and measure the lengths of the table edges.
A movie demo of the illusion by Michael Bach:
http://www.michaelbach.de/ot/sze_shepardTables/
Shepard's "Turning the Tables"
From Michael Bach's "Visual Phenomena & Optical Illusions" This includes a movie: click on the button and you see the shape of one table top moving onto the other merely using translation and rotation -- which you may or may not believe.
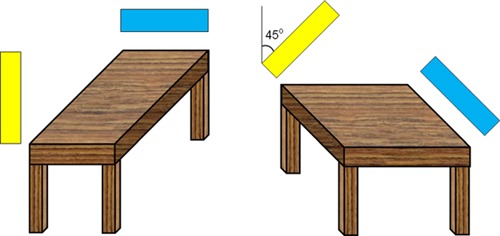
Below is my static elaboration of Shepard's illusion, making it easier for viewers to see that some lengths that look very different are actually identical, using the fact that the two circles were drawn to be identical in size and look identical, making it easier to see which table edges are identical in length in the two sub-pictures.

It may be hard to believe, but each table has one pair of edges equal to a radius of the circle and one pair twice the length of the radius.
The fact that adding the two circles, and the rulers showing the radius and twice the radius, does not remove the illusion helps to clarify the depth of what has to be explained.
I think this is one of very many fragments of evidence showing that common theories about the functions of human/animal vision systems are mistaken, and as a result AI vision systems based on or inspired by those theories are also at worst mistaken, or at best, useful pieces of engineering, but with little overlap with biological vision.
See also the Meta-Morphogenesis project, attempting to unravel what the very many information-processing products of biological illusion actually are, as opposed to which many people think they "obviously" are.
In particular, instead of trying to interpret the optical evidence using (possibly coordinate based) global metrics for length and angle, biological vision makes use of collections of partial orderings, and in general does not automatically detect or eliminate anomalies that result from the inference mechanisms used, because most of the time they work very well -- for biological purposes, which are not necessarily the purposes engineers attempt to give their robots!
As this example shows, there can be more than one system of "measurement" at work simultaneously, in this case the 2-D measures of optical relationships (in what Gibson calls "The optic array") and the system of measurement, or spatial relationships, used in the 3-D interpretation derived from the 2-D information.
A similar point is made in Arnold Trehub's work (e.g. Chapter 14).
The Muller-Lyer illusion is partly similar, partly different. See
https://en.wikipedia.org/wiki/M%C3%BCller-Lyer_illusion
A more general theory will have to account for vision as producing interpretations that are not purely geometrical but include causal and functional relationships, information about the materials perceived (not just their shapes, etc.), information about biological and other classifications of objects and object parts, and in some cases information about states of mind, intentions, purposes, and affective states of other individuals.

This example, with two faces is in part like the Shepard rotating table because for many human viewers (I have not tried a wide range of ages and cultures) the two faces not only appear to express different emotional states, but also differ in how the eyes look, though in this case the difference in appearance is not geometrical. (The eyes in the two images are identical, but here the context changes something more subtle than the geometric interpretation of image contents.)
For more on multi-layer interpretation of visual contents see chapter 9 of
The Computer Revolution in Philosophy (1978).
Identifying evolutionary transitions leading to such types of visual functionality is part
of the task of the Meta-Morphogenesis project.

NOTE:
The image was drawn using William Chia-Wei Cheng's (Bill Cheng's) ancient, but still very
useful drawing program, Tgif. Tgif is an interactive 2-D drawing tool under X11, available
for Linux and most UNIX platforms. (I use it on various versions of Fedora.)

NOTE: This diagram was used, with my permission, in the following book:

William Kaplan, Why Dissent Matters: Because Some People See Things the Rest of Us Miss
McGill-Queen's University Press (June 1 2017)
https://www.amazon.ca/Why-Dissent-Matters-Because-People/dp/0773550704

This web site will be absorbed into the Meta-morphogenesis project's goal of tracing
changes in information processing across biological evolution, development and learning.
http://www.cs.bham.ac.uk/research/projects/cogaff/misc/impossible.html
(On the importance of abilities to see what's possible and not possible.)
http://www.cs.bham.ac.uk/research/projects/cogaff/talks/#agitut
http://www.cs.bham.ac.uk/research/projects/cogaff/misc/meta-morphogenesis.html
http://www.cs.bham.ac.uk/research/projects/cogaff/misc/triangle-theorem.html

Roger Shepard's Rotated Table Illusion Visually elaborated (DRAFT: Liable to change)

Aaron Sloman http://www.cs.bham.ac.uk/~axs School of Computer Science, University of Birmingham.

Previous versions of the illusion online

Recommended Reading (To be expanded)

Roger Shepard's Rotated Table Illusion
Visually elaborated
(DRAFT: Liable to change)

Aaron Sloman
http://www.cs.bham.ac.uk/~axs
School of Computer Science, University of Birmingham.

Recommended Reading
(To be expanded)